How to find horizontal asymptotes? The horizontal asymptote is a y-value present on graphs where a function goes by but never really touches it. The value for why will never be a zero. You can look closely when you see the graph, it will be a zero. They are going to meet the lines and intersect with some values of x and they maintain the same direction. You should know that it is a graph representing a function who will never come in contact.
Related articles about How to find horizontal asymptotes
How to find the area of a trapezoid
How to find the area of a triangle
In this case, both of the polynomials are in second degree. It is the term that contains coefficients and variables that allows the usage of multiplication, addition and subtraction. If you are still not clear, look at the equations below.
x² + 5x + 9 has a single variable which is x.
x³ – 3xyz² + 5 has three variables which are x, y and z.
In the above example, when we said second degree it meant the power of them is square. For example, 4x², 5y² and 8z² are all second degree. If the polynomial is a zero it means that there are not terms at all. If you want to add a polynomial, it is quite simple
A = 3x² + 3x – 5
B = 6x² + 4x + 8
A + B = 9x² + 7x + 3
Here is how you can find the horizontal asymptote of the example given above,
Y = which means y = 6.
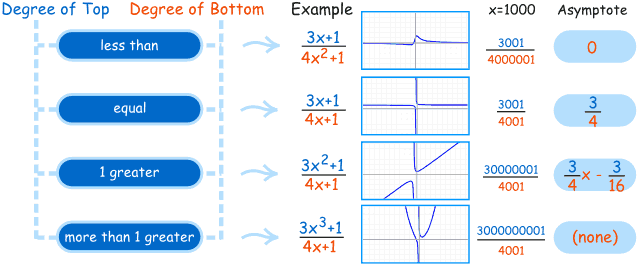
When the polynomial is at different degrees, meaning the numerator has a value of x² and the denominator has a x without any power, then there is no horizontal asymptote.
Here is an example,
We can see that 12 has x and the x has a power of 2 or square. The denominator does have an x which does not have a power. Therefore, the result for this one is that there is no horizontal asymptote.
Here is another case,
Do not confuse them or get scared. Look closely at the degrees. The first step is to look at each of the values you have. It is the easiest one because you can see that the numerator has a less degree than the denominator. Here, the result is going to be y = 0. Whenever, you get a question where they have asked you solve the horizontal asymptotes of rational functions, look at the degrees. You will have three kinds of results. One is simplification.
Here is another example
Since, you know all the rules now, it should be easy to solve. You can see that both of them has square as the power. 15 and 5 are divisible. You can either write y = or if the teacher asks you to write in the shortest term possible, simplify as much as you can. The result with be 3.
Tips
• The teacher may ask you draw a graph, for y = 3, draw a straight line using your scale on the y-axis where it is 3.



