There are six variations of quadrilaterals—rectangle, parallelogram, rhombus, kite, trapezoids, and squares—and with the exception of a rhombuses and kites, each has a different method for calculating the area. The area of a quadrilateral is the number of square units on its surface, which is a figurative way of saying “the space between the lines”. To simplify, think of an area rug. The amount of space it takes up on your floor is its area. Abstract shapes are no different, and square units have virtually unlimited practical use in complex mathematics. A trapezoid is a type of polygon called a convex quadrilateral, which means it is a shape of four sides with at least two of these sides running parallel to each other. It is similar to a parallelogram, which has two pair of parallel sides, and a rectangle, which also has two parallel sides but all right angles. However, the area formula has slight variations, which we will discuss below.
Related articles about How to find the area of a trapezoid
How to find the area of a circle
How to find horizontal asymptotes
The formula for finding the area of a trapezoid is base plus base times height, divided by two, or:
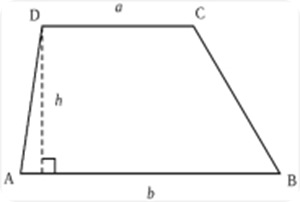
Observe the image of the trapezoid on the right to identify the which lines are which. Despite base implying the bottom line, it actually refers to both the horizontal line at the top and the one at the bottom. The height requires measuring the length from base to base, which unlike a square, is not always the same as the length of the sides because they can be at angles that make them longer. Notice that the measurement for height, marked h, was taken using the right angle between the bases (a and b), instead of the line between angles D and A. To find the area of the pictured trapezoid and any other, you would follow these steps:
1) Find the length of lines a and b and add them together.
2) Take the result of that, and multiply it by the length of line h.
3) Divide the result of the first two steps by 2.
When calculating the area of a trapezoid, it is important to follow order of operations in this formula as it is with all mathematical procedures. If you’re not familiar with order of operations, memorize the PEMDAS method to help you remember which to do first. This one’s pretty straightforward because it has parenthesis to show which one comes first (the P in PEMDAS), but many mistakes are made for doing one step before the other in a math problem. You may also encounter problems where some of the numbers are missing and you need to find additional methods to calculate their values before you can complete the equation, though in most situations it is acceptable to substitute the variable x for unknown quantities and leave it as such in the answer. For example, in this problem we don’t know the length of the first base: = =
When we figure out that the value for x is 6, it we can plug it in: =